The Mohr Circle
Geologists and engineers calculate normal and shear stresses from the orientation and magnitude of two of the three principal stresses using the Mohr diagram. This diagram graphically illustrates in two dimensions the complex mathematical relationships between the components that make up a traction. Software for graphing the Mohr diagram is provided in Visualizing Stress. However, before using the software to analyze various states of stress, the components that make up the Mohr circle must be first explored.
The fundamental stress equations derived in the previous section (Equations and ) can be rearranged as follows. For normal stress (sn)
![]()
and for shear stress (t)
![]()
Squaring both sides of Equations and reveals
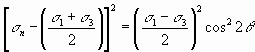
and
![]()
Combining Equations (49) and (50) yields
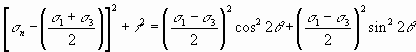
Simplifying
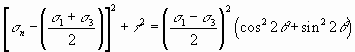
Now recall the trigonometric relationship ![]() .
Substituting this relationship into the right hand side of equation results
in
.
Substituting this relationship into the right hand side of equation results
in
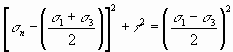
Recall from your college algebra class that the equation of a circle drawn in an x-y coordinate system is
![]()
where r is the radius of the circle and (h, k) are the coordinates of the center of the circle. Comparing Equations and reveal that the fundamental stress equations define a circle in sn-t space centered on the point
![]()
with a radius of
![]()
Figure 17 illustrates a circle constructed from Equation . The circle represents the locus of all possible normal and shear stresses for a given state of stress acting on planes whose normals make an angle of q degrees to s1.
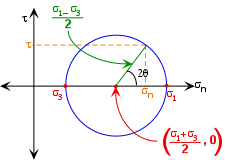
Figure 17. The Mohr circle constructed from Equation with a radius defined by Equation and a center with the coordinates in Equation.
Structural geologists refer to Figure 18 as a "Mohr circle" after the German engineer Otto Mohr (1835-1918) who first introduced them over a century ago. Note further that the average stress is simply
![]()
or, in three dimensions
![]()
In a Mohr diagram, average stress is the center of the Mohr circle. Differential stress is the difference between the maximum and minimum principal stresses. In a two dimensional Mohr diagram differential stress is the diameter of the Mohr circle.