Normal and Shear Stress
The traction's on the planes that intersect at the origin of Figure 12 can be subdivided into perpendicular and parallel components to each plane. The component perpendicular to each plane is termed normal stress (sn) and the component parallel to each plane is termed shear stress (t). Figure 14 illustrates the relationship between the traction (s) and the normal (sn) and shear stress (t) components acting on a single plane whose trace in two dimensions the line segment AB.
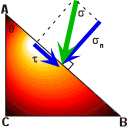
Figure 14. The two-dimensional trace of a right triangular prism with normal (sn) and shear (t) stresses acting on the plane defined by line segment AB. The normal and shear stresses are the components of the traction, s .
The normal and shear stresses can be calculated on a plane of any orientation if the magnitude and direction of two of the three principal stresses (s1, s2, and s3) are known. In Figure 15 the normal stress, sn, and shear stress, t, are acting on the trace of a plane defined by the line segment shown as AB in Figure 14. In Figure 15, the principal stresses, s1 and s3 are oriented perpendicular to the legs AC and BC, respectively of the right triangle ABC.
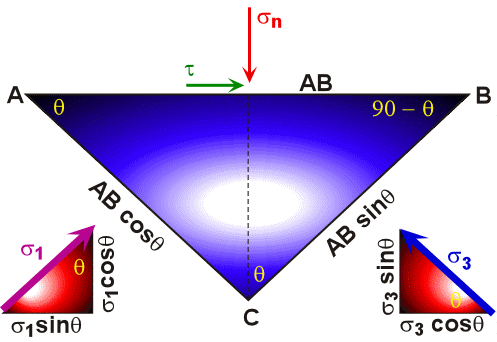
Figure 15. The graphical relationship between the normal, sn, and shear stress, t,and the two principal stresses, s1 and s3.
The equations for normal and shear stress are commonly referred to as the fundamental stress equations. Assuming static equilibrium and using the relationships illustrated in Figure 15, derivation of the fundamental equation for normal stress begins with the balancing of forces where:
![]()
Canceling similar terms and simplifying:
![]()
Substituting the trigonometric identities ![]() and
and ![]() into
Equation (40) yields:
into
Equation (40) yields:
![]()
Further simplification reveals the standard form of the equation for normal stress:
![]()
Again, assuming static equilibrium and using the relationships illustrated in Figure 17, derivation of the fundamental equation for shear stress begins with the balancing of forces where:
![]()
Canceling similar terms and simplifying:
![]()
rearranging terms:
![]()
substituting the trigonometric identity ![]() into Equation (45) yields the fundamental stress equation for shear stress:
into Equation (45) yields the fundamental stress equation for shear stress:
![]()