Homogeneous and Heterogeneous Strain
Mathematical treatments of strain commonly assume homogeneous rather than heterogeneous distortions or strains. However, any heterogeneously strained rock body can be subdivided into small areas that exhibit the characteristics of homogeneous strain. Heterogeneous strain affects non-rigid bodies in an irregular, non-uniform manner and is sometimes referred to as non-homogeneous strain (Figure 28). During heterogeneous strain parallel lines before strain are not parallel after strain, while circles and squares or their three-dimensional counter parts cubes and spheres are distorted into complex forms. Homogeneous strain affects non-rigid rock bodies in a regular, uniform manner (Figure 29). During homogeneous strain parallel lines before strain remain parallel after strain, as a result cubes or squares are distorted into prisms and parallelograms respectively, while spheres and circles are transformed into ellipsoids and ellipses respectively. For these generalizations to hold true, the strain must be systematic and uniform across the body that has been deformed.
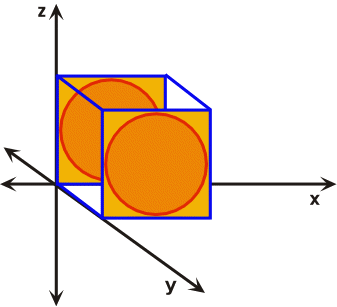
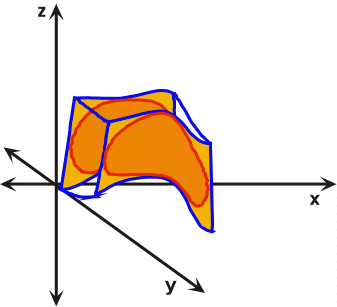
Figure 28. Heterogeneous or non-homogenous strain results in distorted complex forms.
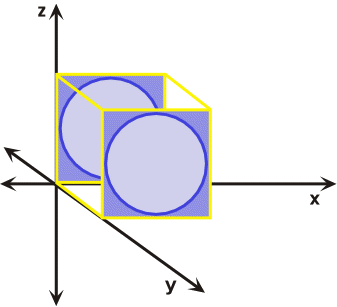
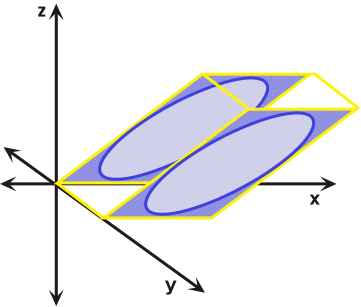
Figure 29. Homogenous strain affects bodies in a regular and uniform manner.