Lithostatic Stress
Let us now consider a problem formulated by Means (1976) and discussed vividly by Davis and Reynolds (1996). The problem, simply stated, is what would be the stress on a horizontal surface 1500m by 1500m across at the base of a 3.375x109m3 cube of granite in the upper crust (Figure 5)?
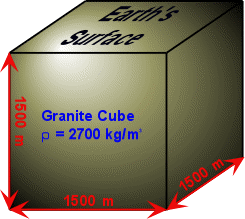
Figure 5. Cube of granite in the Earth's upper crust with a uniform density of 2700 kg/m3 and a volume of 3.375x109m3.
As illustrated in Figure 5, the cube of granite extends from the Earth’s surface to a depth of 1500m and has a uniform density of 2700 kg/m3. The force generated by the weight of the overlying cube of granite is
![]()
where r is density, V is volume, a, is the acceleration due to gravity, and F is force. Substituting the values taken from the problem formulated above yields
![]()
which upon multiplying out reduces to 8.93 ´ 1013 kg×m/s2 (or N). Recalling from our previous discussions that stress is force acting over some surface area, we divide this value by the area of the base of the cube of granite,
![]()
or 39.69 MPa.
As you may have guessed by now, the question set up by Means (1976) and Davis and Reynolds (1996) is used to illustrate the concept of lithostatic or confining pressure. The stress along the base of the column of rock in Figure 5 was resolved following the principles defined in Equation (9). Recall the definition of stress from Equation (1)
![]()
where s = stress, F = force, A = area, m = mass, and a = acceleration. The stress at any point within the granite cube in Figure 5 can be resolved with the equation for lithostatic stress
![]()
where r = density, g = acceleration due to gravity, and h = height of the overlying column of rock above the point in question. Equation can be simplified to the more familiar definition of stress in Equation by defining the individual parameters that make up the equation:
![]()
where V = volume. Simplifying further:
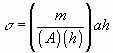
and then canceling terms yields
![]()
Simplifying further and resolving for the force (F) reveals the familiar definition of stress:
![]()