Normal and Shear Stresses at Failure
The Mohr Circle can be used to evaluate the normal and shear stresses acting on a plane whose normal makes an angle of q degrees to the maximum principal stress, s1. For example, Handin (1966) provides the results of a triaxial stress test on a sandstone from Berea, Ohio. The specimen failed under a confining pressure of 500 bars and a differential stress of 1590 bars. Temperatures during the experiment were maintained at 24o C. Recall from earlier discussions that differential stress is equal to s1-s3. We then write s1-s3 = 1590 bars. During the triaxial stress test, the confining pressure was kept equal to s3. Therefore s1 = 1590 bars + 500 bars = 1640 bars. When the specimen failed, it broke along fractures oriented at 27o to s1. This angle is commonly referred to as the fault angle. Theta (q), the angle between the normal to the plane of fracturing and s1 is thus 90o-27o=53o. These relationships are portrayed in Figure 19, and can be plotted utilizing the procedures described in the previous section.
For example, select New from the File menu. Then enter for Sigma1, 1640, for Sigma3, 500, for Theta, 53o, and for Pore Pressure 0. Next select Graphics, followed by Plot Controls. Select Mohr Circle check the box labeled Stresses. The normal and shear stress acting on a surface oriented at 27o to s1 at failure are plotted on the Mohr circle as a small bold point (Figure 20).
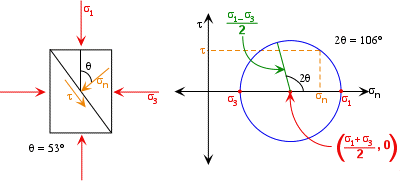
Figure 19. The relationship between the principal stresses, the normal stress, shear stress, and theta, are illustrated for a block diagram on the left for a Mohr diagram on the right.
Figure 20. Mohr circle with the normal and shear stress at failure plotted as the bold point.