The Stress Tensor

In the previous section we solved for the lithostatic stress, or the stress caused by the weight of an overlying column of rock on its base. What if there were some modest tectonic stress oriented East-West in addition to the lithostatic stress? In order to answer this question we need to set up an arbitrary coordinate system where the x-axis is horizontal and the z-axis is vertical (Figure 7). At the base of the granite cube the vertical stress will be the lithostatic stress that we calculated in the previous sections, but we will round the calculated value off to 40 MPa for the sake of simplicity. Parallel to the x-axis is our modest tectonic stress which, following Davis and Reynolds (1996), we will assign a value of 20 MPa. In order to calculate the stress at the base of the granite cube produced by the given set of conditions we need to calculate the tractions acting on every possible plane that could conceivably pass through a discrete point! Though such a task may seem daunting at first glance, with a little thought and the aid of a modern day computer, the task can be reduced to a few minutes of work.

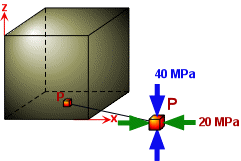
Figure 7. Point P is located at the base of a granite cube in the upper crust with a vertical stress of 40 MPa and horizontal stress of 20 MPa.

To better understand the principles behind the task at hand, let us begin by calculating the stress acting on a single plane passing through a discrete point (P) at the base of the granite cube. If we take point P to be a cube with dimensions of millionths of a meter, a plane oriented q = 50^o from the z-axis of that cube will have an area of intersection equal to some finite number n m² (Figure 8). The right triangular prism formed by the plane passing through point P in Figure 8 will have the two dimensional trace ZX in Figure 9. Line segment ZX in Figure 9 is the hypotenuse of a right triangle with legs represented by line segments ZO and OX which are parallel to the z and x-axes of our coordinate system. XZ is n x 10^-6 m long, while ZO and OX are 10^-6 m long. Thus, (1) the area of the face of the triangular prism that is perpendicular to the z-axis is labeled Area_OX and is equal to:

(18)

(2) the area of the face of the triangular prism that is perpendicular to the x-axis is labeled Area_OZ and is equal to

(19)

and (3) the area of our plane of interest is labeled Area_ZX and is equal to

(20)

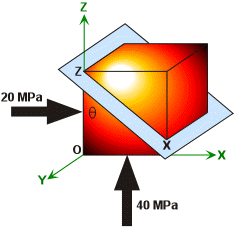
Figure 8. Point P as a cube with dimensions of millionths of a meter. The plane passing through point P creates a right triangular prism on which our stresses are acting.

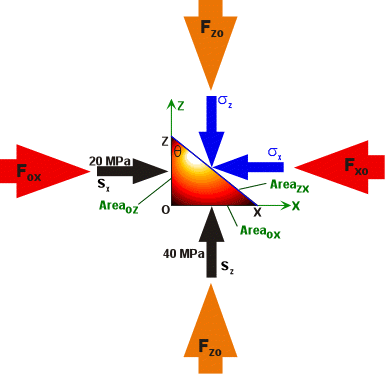
Figure 9. The two dimensional trace of the right triangular prism created by the intersection of point P with a plane q degrees from the z-axis. S_x is the horizontal stress in the OX direction and is equal to 20 MPa. S_z is the vertical stress in the OZ direction and is equal to 40 MPa. s_z is the vertical stress in the ZO direction and s_z is the horizontal stress in the XO direction. The forces (F) in their respective directions are resolved from the stress in the same directions divided by the areas of the faces of the right triangular prism on which the force is acting.

We now assume that all of the forces acting on our right triangular prism are balanced. Recalling that stress is force divided by area we can then write

(21)

(22)

and

(23)

Again rearranging terms

(24)

where F_OX is the force acting in the OX direction, F_XO is the force acting in the XO direction, AreaOX = (AreaZX)(sin50o), and S_x = 20 MPa. If we are in a condition of static equilibrium, then

(25)

or

(26)

Simplifying further

(27)

Rearranging, canceling similar terms, and isolating s_x:

(28)

Solving for s_z involves a similar set of steps. First we write

(29)

(30)

and

(31)

(32)

where F_OZ is the force acting in the OZ direction, F_ZO is the force acting in the ZO direction, , and S_z = 40 MPa. If we are in a condition of static equilibrium, then

(33)

or

(34)

Simplifying further results in

(35)

Rearranging, canceling similar terms, and isolating s_z gives

s_z and s_x are the components of the stress vector or traction, s_xz acting on Area_zx. To solve for the magnitude of this traction we use the Pythagorean theorem,

As shown in Figure 10, b is the angle that s_xz makes with the s_z and is equal to

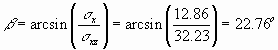
Thus, s_xz is the stress vector or traction with a magnitude of 32.23MPa oriented 22.76^o clockwise with respect to the s_z on a plane oriented at 50^o to the z-axis produced by a vertical stress of 40MPa and a horizontal tectonic stress of 20MPa. What would the magnitude and orientation of every other possible traction be to point P? In other words what is the stress tensor?

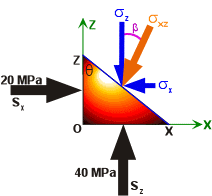
Figure 10. The stress vector or traction, s_xz, has a magnitude of 32.23MPa oriented 22.76^o clockwise with respect to the s_z on a plane oriented at 50^o to the z-axis produced by a vertical stress of 40MPa and a horizontal tectonic stress of 20MPa.