In order to answer the question posed at the end of previous section we use the Stress Tensor Calculator in Visualizing Stress. Select Stress Tensor from the Calculators menu in order to initialize the stress tensor calculator. In the Stress Tensor Controls dialog (Figure 11) enter 20 in the textbox labeled SigmaX and 40 in the textbox labeled SigmaZ then select Plot. SigmaX and SigmaZ are analogous to horizontal stress S_x and vertical stress S_z respectively in the previous section.

Figure 11. The Stress Tensor Controls dialog box.

Visualizing Stress calculates s_xz on a set of planes that form a circular fan about point P, each plane being separated from its neighboring plane by 5^o. The tails of the vectors defined by s_xz form the ellipse in Figure 12. Visualizing Stress puts the data used to calculate the tractions on each plane in a table next to the stress ellipse shown in Figure 12.

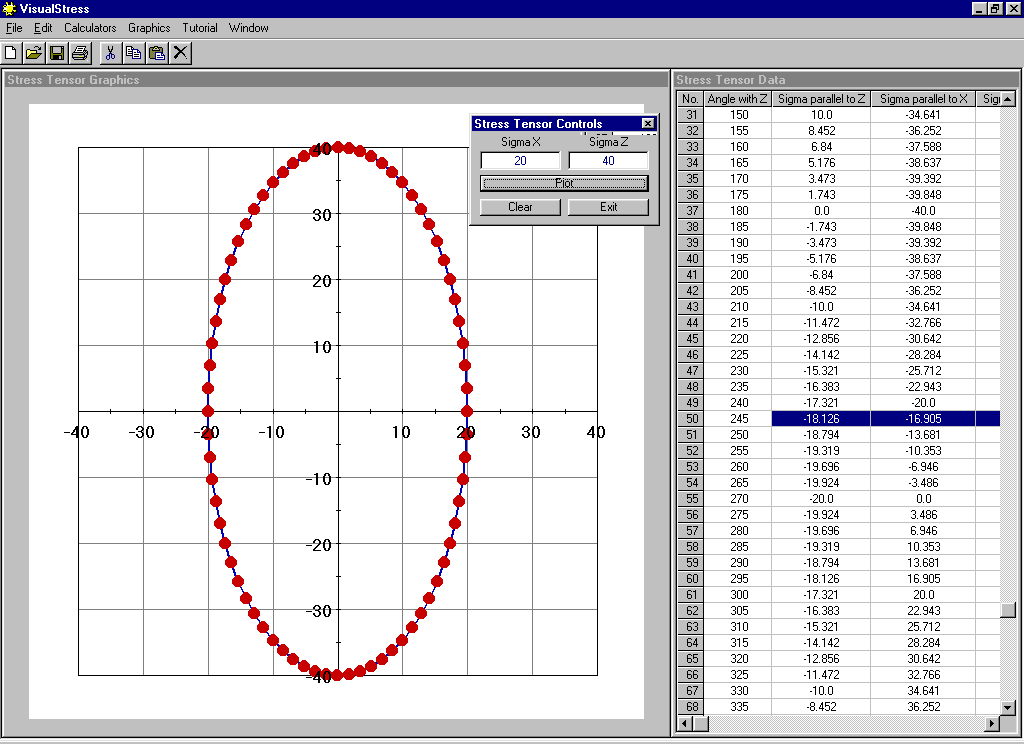
Figure 12. Each red dot in the ellipse defines the tail of each traction, s_xz, acting on the set of planes that form a fan about point P. Each plane is separated from its neighbor by 5^o. The table of data created by the Stress Tensor Calculator was used to solve for the tractions about point P.

The magnitude and direction of s_xz can be visualized by imagining a line running from each plotted point to the origin of the XZ coordinate system. Note that the distributions of s_xz forms an ellipse which structural geologists refer to as a stress ellipse (Figure 12). Moreover note that there are two mutually perpendicular directions of s_xz that represent the largest and smallest magnitude stress vectors. These two stresses are referred to as the maximum and minimum principal stresses. In three dimensions the stress ellipse becomes an ellipsoid with three mutually perpendicular principal stress directions, referred to as s₁, s₂, and s₃ (Figure 13). Structural geologists refer to s₁ as the maximum principal stress, s₂ as the intermediate principal stress, and s₃ as the minimum principal stress. Thus, if we view a section perpendicular to one of the three principal stress directions, then the section that we are viewing will contain either (s₁, s₂), (s₁, s₃), or (s₂, s₃). Furthermore, as will be discussed in the next section, if we know the orientation and magnitude of two of the three principal stresses, then we can calculate the normal and shear stresses acting on all possible planes oriented at some given angle to the known maximum principal stress.

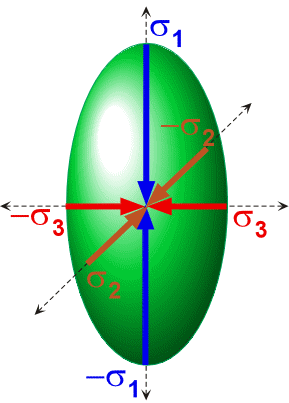
Figure 13. The stress ellipsoid with the three mutually perpendicular principal stresses, s₁, s₂, and s₃.

<< contents >>