Traction
What we are calling "stress" is more accurately termed "traction." A traction is a force per unit area acting on a specified surface (Figure 1). This more accurate and encompassing definition of "stress" elevates stress beyond being a mere vector, to an entity that cannot be described by a single pair of measurements (i.e. magnitude and orientation). "Stress" strictly speaking, refers to the whole collection of tractions acting on each and every plane of every conceivable orientation passing through a discrete point in a body at a given instant of time (Davis and Reynolds, 1996).
A traction is a vector quantity, and, as a result, it has both magnitude and direction. These properties allow a geologist to manipulate tractions following the principles of vector algebra. Like a traction, a force is a vector quantity and can be manipulated following the same mathematical principals. For example, consider some force, F, acting parallel to the y-axis on line segment AC illustrated in Figure 3. Now ask the question, what are the components of this force acting normal and parallel to line segment AC? In order to answer this question, we must resolve F into its two vector components Fn and Fs. Fn is the component of F acting normal (perpendicular) to AC and Fs is the component of F acting parallel to AC. Fn is referred to as the normal force whereas Fs is termed the shearing force. Trigonometric relationships displayed in Figure 3 indicate that
![]()
and
![]()
where q is the angle between Fn and F.
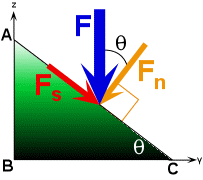
Figure 3. The force, F, acting on line segment AC can be resolved into a normal component (Fn) and parallel component (Fs) to line segment AC.
In similar fashion we could ask what are the normal (sn) and shear (t) stresses acting on the face AA'-A'C'-C'C-CA of a right triangular prism as shown in Figure 4? Another way of asking the same question would be to ask what are the normal and shearing tractions acting on the surface defined by AA'-A'C'-C'C-CA? A traction then, is a component of a stress vector acting on a specified plane (Figure 4).
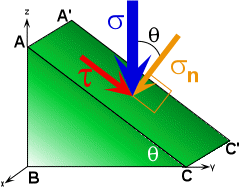
Figure 4. Traction, s, acting on the area defined by the plane AA'-A'C'-C'C-CA can be resolved into a normal component (sn) and parallel component (t).
Remembering the definition of stress and the reviewing the reasoning used to evaluate Figure 3, close scrutiny of Figures 4 reveals
![]()
and
![]()